2019-05-04
Part of a series about
Grass, a real-time roguelike engine with pretty graphics.
I'm currently working on Grass, a roguelike engine / game / thing. It's nothing concrete yet, but I realized I have things to say about it. Let me start from the beginning, though.
My history with roguelikes
Back when I was 11, I read a newspaper article titled "Does @ have a soul?". It described a fascinating game called NetHack, in which you can play as an @ sign, monsters are letters, the possibilities are endless, and people keep trying to win the game for years.
I had a 386 computer with MS-DOS at the time and I spent a lot of time playing NetHack, even printed the "Guide to Dungeons of Doom" on paper to learn all the commands. I never won, and after some time I moved on to ADOM after reading about it on one of the Polish websites.
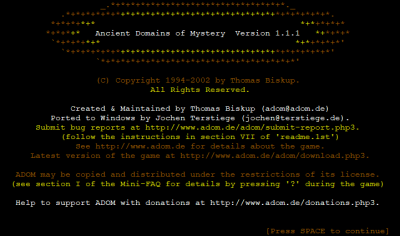
ADOM pulled me in for a very long time. After several years of playing it on-and-off, over a particularly long summer break (the one after finishing high school!), I finally started winning.
In many ways, ADOM is a flawed game, but it's also extremely rewarding. I have many happy memories with it. I rescued the tiny girl's puppy countless times. Saved the world… not so many times, but still got to do it with different characters and play styles. I still have the character dump for every one of my winning characters. They also all got posted to Polish ADOM forum, a (long dead now) phpBB based community where I made some long time friends.
And since the earliest days of NetHack, I always wanted to make my own roguelike.
ASCII graphics
The graphics in a roguelike depend on a convention. @ is usually your player, r is a rat, g is a goblin, # is a wall, and so on. You need to learn the convention at first, but then it gets really immersive. Encountering an upper-case D can be really scary, because you know that D means a Dragon and that it's really easy to lose a fight against one (and did I mention there is no restarting from a saved game?)
I vividly remembered the first time I entered the Tower of Eternal Flame. I was so nervous I almost physically felt the heat.
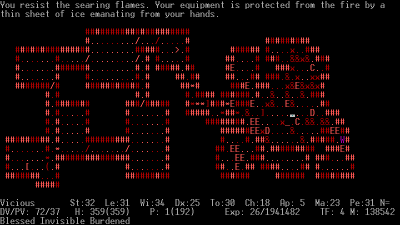
I would compare ASCII graphics to something like chess diagrams. There are a few easy-to-distinguish characters, which you are not supposed to interpret as pictures, but as symbols with a meaning.
That does not mean the graphics cannot be pretty by themselves. Using the right font and colors can do a lot for my enjoyment of the game.
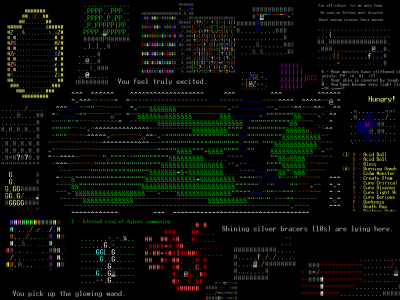
Alternatively, a roguelike game can have a set of graphical tiles. I used to be skeptical because I really like clean, recognizable symbols, and stylistic consistency. Tiles are often less recognizable and make the game uglier. But I've seen some cases where it's done pretty well.

(Dwarf Fortress tileset)
Making my own
Like any roguelike developer, I have many half-formed ideas for my own game. I tried to come up with an engine many times, as I was learning various technologies: C++, Common Lisp, D…
Getting stuck in the initial phase, and "analysis paralysis", is pretty well known in roguelike world. There is just too much freedom! So many ways things can go, and so many features to add! One way to overcome this problem is the Seven Day Roguelike challenge, in which you force yourself to finish something in 7 days. You will not finish your huge project, but you will release something instead of being stuck.
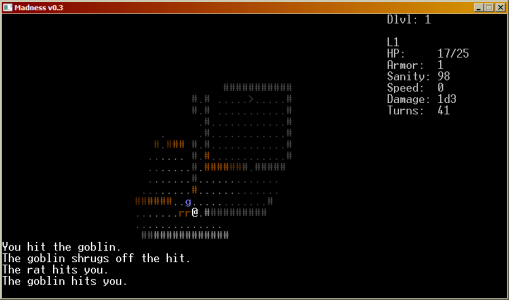
I participated in the 7DRL challenge in 2010, creating Madness, a small game in Python with hallucinations and other visual effects. It was a pretty intense week, with a lot of feature-building at the beginning, and a lot of play-testing and balancing the game towards the end.
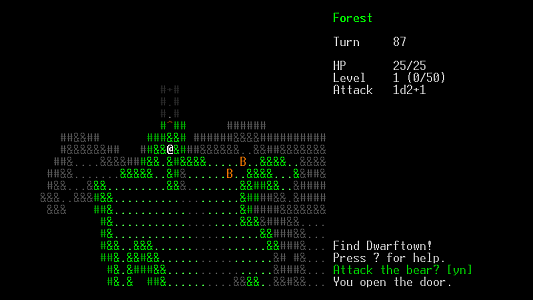
And I did it again in 2011 with Dwarftown, a slightly less successful project where I learned Lua, experimented with lighting (torches on the walls!), various map generation techniques (including a dungeon made of Tetris pieces) and Angband-inspired health bars.
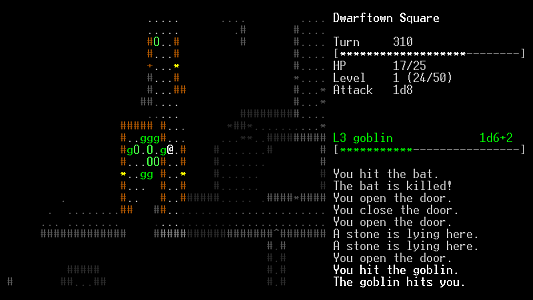
Grass is another attempt at a roguelike. It's not as advanced but I'm enjoying myself so far…
2019-02-24
Here is what I learned about running workshops. This is based on various sessions I ran, most of them about programming in one way or the other. Hopefully, some of the ideas will be applicable to other workshops as well.
I hope my advice will be useful, but no guarantees: these are things that worked out for me; your needs, topic, students, or teaching style might be completely different.
Scope of the workshop
You probably have a topic in mind, but what exactly are you going to teach? Surely you will not show your students everything you know about the topic.
You could give them a "teaser". Show the most interesting parts, so that they will want to learn more. And even if they won't, you will leave them with a memorable experience.
Or, you could aim for a good "foundation". What are the 2-3 most important, core ideas from your field? Maybe a technique, or a viewpoint, that the students will recall later? Something on which they will be able to build.
In any case, prefer quality over quantity. You already understand these things, they don't, so keep yourself from going too fast. Better to explain a few things well, than gloss over many.
Structure
Exercises are the most important part. This is the opportunity for your participants to work on something, and learn by doing. For this to be effective, you should first give them tools: explain the background, make them understand concepts.
Usually that means a bit of theory, then an exercise, then more theory, another exercise and so on. Or just exercises building one on another.
Start with motivation: what is this thing for? For instance, in a workshop about test-driven development, take a few minutes to explain why we write tests.
Consider giving a homework before the workshop. That's not always possible, but when it is, it gives students some background. For instance, for my workshop about FPGAs and logic design, I ask students to prepare by playing the NAND Game which will teach them about logic gates.
Be prepared
It's tempting not to prepare too much, and just improvise. And it might just work, if you know what you're teaching by heart! Still, if you can afford the time, it will make the workshop go much smoother.
Have a rough plan written down. This way you won't forget anything important, and you'll notice if the list of topics gets too long.
Do the exercises yourself first. Don't give an exercise you haven't solved! You might find out it's unsolvable, too hard, or just not what you meant. A few times, the only thing that didn't work out in the whole workshop was the last-minute addition that I haven't rehearsed.
If you'll be using some software, be prepared to help the participants install it. Tell them before workshop what they will need. Plan for differences between systems: Linux / OS X / Windows, different code editors, and so on. In one extreme case, I prepared a VirtualBox image with all the software, to avoid problems with individual setups.
Have a written script
A well-written script will be invaluable for your students, both during the workshop and after. Nowadays, I usually create a GitHub repository with workshop script and code.
Your script should contain all your exercises, and everything your students might need to refer to: code to copy-paste, links for software to install. It's much easier when you can point to the script – instead of repeating the same instructions, you can focus on explaining them.
You can also add more links for further reading, and additional "bonus" exercises. That doesn't cost you much, and the interested participants have something useful to follow after the workshop.
Keep in mind that your materials could help someone else give the workshop. They will also be indispensable if you repeat it yourself in a few months.
Starting code
If your tutorial is about programming, prepare some skeleton code for the exercises, so that it's easier to start coding. Same goes for Makefiles, project boilerplate, or anything else that helps get them up and runing faster.
Consider also adding unit tests, so that the students can check their exercise. A fancier variant of unit tests is a "judge" program. For instance, in a multi-threading workshop I have a judge that measures how many requests per second your code is processing, and checks if it's doing anything forbidden.
As mentioned before, you should solve the exercises yourself. You can include the solutions with the code. I keep them as another Git branch called reference.
Live coding
The common wisdom is that live coding is very risky and you should avoid it during presentations, because you will likely fail. I maintain that it's usually because people don't put in enough effort to prepare and rehearse.
And while things might still go wrong, I think the end result is well worth the risk! People will pay more attention and understand more of what you're doing. You will be able to "show, not tell".
I had some successes even with longer (~ 45 minutes) live coding presentations. I rehearse them at least 2 times: once to try things out and work out the details, then again to make the it faster and more fluent.
Once I did a pair live-coding session with a student. It was a pair-programming TDD exercise. We rehearsed it a few times (and decided to present on student's laptop, not mine), and the end result was pretty impressive.
Exercises
The exercises shouldn't be too hard. Plan for differences in level. Chances are some people will not solve the exercise, and some will finish it quickly and be bored. (You can have some extra "bonus" tasks for the second group).
Walk around, observe people working on the exercises. Help them if they're stuck. Answer questions. Give hints. Don't spend too much time on one person while others are waiting. Your attention as mentor is crucial at this stage. This is the main part of the workshop: make sure people get out as much as they can.
Before moving on to the next part, explain the exercise to everybody (or better, make someone else explain, but correct them if necessary). This will be useful to people who didn't manage to finish, but also for people who did finish but arrived at a different solution, or have some misconceptions.
After the workshop
The workshop has ended. Now is your chance to learn something about your teaching methods. Don't waste it!
Ask your participants for feedback. I try to send a Google Form with a few questions: what did you like? what went bad? do you have any suggestions for me?
You can also write down your own impressions while they're fresh.
Then, decide how to improve the workshop, update the materials, and get ready for the next edition!
2019-01-01



Chaos Communication Congress is a huge, amazing meetup of hackers, artists, makers, activists, anarchists, and other like-minded people. I just returned from the 35th edition, held in Leipzig, Germany. It was the 3rd Congress I attended, and as always I was hugely impressed by the feeling of being a part of greater community. This is a completely different event than commercial IT conferences and you can tell that these people are here to work together and help each other, not only talk about what they are doing for their employer.
I took a lot of photos, although I was careful not to include any people in the picture – the congress rules say you are not allowed to take people's photos without their consent. There is a lot to photograph on CCC other than people, though :)
You can find most of the main talks recorded at media.ccc.de. I watched too many talks to list here, but I will describe some that I liked best.

Planes and Ships and Saving Lives was a talk by Mission Lifeline, one of the last organizations out there rescuing the refugees trying to cross the Mediterranean Sea.
They talked a lot about both the political problems they were facing trying to get the European governments to respect basic human rights and not leave people out to die at sea. The technology was also mentioned – having to manage laptops and other devices on a ship is somewhat harder than doing the same thing on land. For instance, they manage all the laptops using Ansible, so that they can quickly configure a new laptop if one fails. They also keep really good documentation, in case they need to do some troubleshooting while at sea with weak (if any) Internet connection.
For me, the definite highlight of the whole CCC was the live call during this talk. We connected with the SeaWatch 3 crew that rescued 30 people a week before, and were still looking for a port that would take them in. "A lot of people" were negotiating on their behalf, but no luck so far.
Tactical Embodiment was given by Angela Washko, an activist exploring various online spaces that are hostile to women. She was presenting The Game: The Game, a visual novel game about the pick-up artist community, where you could experience how is it to be a target of PUA gurus' pick-up methods. The game is very well researched, and everything the characters do is based on their "training materials" from real life. The end result is pretty unsettling and difficult to watch (a lot of creepy behaviours ranging from unwelcome advances to outright sexual harassment) but very valuable.
Among more technical talks there was Space Ops 101. That talk was a detailed (but still pretty accessible) description of how a satellite is launched and operated from the ground. I learned many interesting details about different orbits, launch phases, problems and recovery, mission planning, and decommissioning a satellite after it reaches end of life.

Recently, I'm playing with FPGA chips (programmable circuits, designing your own processor, etc.), and right now there is an open source FPGA revolution going on (with the IceStorm toolchain), so it was great to see all these people making FPGA tools and boards on CCC. I bought an IceBreaker board, and I would like to recommend Snakes and Rabbits - How CCC shaped an open hardware success, in which two indie hardware makers talk about building open source hardware.
At Taming the Chaos, I learned about current work in securing software written in C. The author is part of CHERI project that aims to create "hardened" processors that would detect common C out-of-bounds pointer bugs. He also talked about creating formal, executable specificiations for processor ISAs (instruction set architectures).
Ultimate Mars Rover Talk is definitely worth watching. The talk is about Mars Curiosity rover, what software it's running, and how it's operating on Mars surface. By the way: the "Ultimate (…) Talk" series is pretty great. If you're not afraid of low-level details, last year's Ultimate Apollo Guidance Computer will leave you speechless.

Finally, A Christmas Carol - The Spectres of the Past, Present, and Future is an impressive summary of various Meltdown and Spectre exploits. The "main character" is visited by three Spectres and they came to a rather scary conclusion: these kind of attacks will probably keep us busy for a very long time.
2015-10-03
AgileByExample was a Warsaw conference on agile software development. I attended two days of workshops and learned a few new things about communicating with people, organizing work and developing a product – overall, time well spent.
The talks were organized by three tracks: team, product and business. Here are some things I noted down.
-
There was a lot of emphasis on intrinsic motivation (as opposed to motivating people with rewards and penalties). As a general rule, assume people are as productive as the system allows them to be (and try to change the system to give them more freedom / sense of purpose).
-
Also, remember that programming doesn't look like work! Worth to keep in mind that when a programmer is trying their hardest, they usually look like they're daydreaming.
-
Another big topic was work in progress and how to limit it. The main insight I got is that having a lot of unfinished work is not only a scheduling and efficiency problem – if your organization is overloaded with work, it's also limiting your ability to see the big picture and make more conscious changes.
-
Treat product changes not as projects, but as bets! Thinking about what to bet on is a completely different mindset than creating a schedule for a project, and forces you to think more about the expected value than low-level planning.
-
While we're on product changes, impact mapping (example) is also a good way to hierarchically present a plan, so that the focus is on goals, not only individual features.
-
If you really want to convince people, you have to take care of their safety and appeal to them both on rational and intuitive/emotional level (convince both the "elephant" and the "rider"). To make a more powerful argument, draw what you're talking about. Another idea: games or simulations that illustrate your point.
-
Drawing is generally a useful communication tool to have. Have a look at Bikablo for some clever shortcuts.
-
There was an interesting talk on root cause analysis. The author presented a very methodical approach of drawing the whole branching diagram of causes (his team even used a mind-mapping software instead of just whiteboard!) You have to be careful of jumping too quickly to conclusions, and of presenting opinions instead of facts – as a result of these, it's easy to miss something important about the situation.
-
Belbin Team Roles sound like an interesting way of analyzing teamwork. I will have to read about them.
-
Improv exercises. This is not the first time I hear about them in the context of agile. I will have to read about them.
-
Idea: don't demo your software to the customers. Just give it to them and let them use it themselves. You will learn a lot from watching them.
2015-08-29
This short book may have been written for system administrators, but as a software engineer I found it no less helpful. In fact, there is not much content specific to technology, either. What you will find inside is a bunch of "street-fighting" techniques for managing your time that you can use whenever you find yourself juggling many tasks and requests from other people; regardless of what your actual job is.
The author describes a simple system of preparing a to-do list for a given day, then moving any "spilled over" tasks to the next day, as opposed to having a huge ever-growing master list that you will never clear. There is interesting advice regarding prioritization: apart from estimated effort and urgency, you have to also consider what delivery time your customer is expecting. If they know you can do it in 5 minutes, better do it soon. If you can do it in 5 minutes but they only expect it the next day, you can start with something more important.
Another good piece of advice is to avoid conscious thinking about things that you can do often, but "solve them once and for all" by making them routine. For instance, the author always holds the car keys in one hand while closing his car: he has incorporated an "automated check" that helps him avoid locking the keys in. Another example would be always doing some things (like buying new supplies, or doing your laundry) at a given day of week, instead of constantly worrying about when exactly you need to do it.
For a more sysadmin-specific example: whenever you're adding a firewall rule, first verify that whatever you want to block is NOT blocked, then add a rule, then check whether it's blocked now, so that you're sure your rule blocked the right thing. The practice should sound very familiar to programmers writing automated tests: first, write a test and make sure that it fails. The same applies to reproducing a bug before you go on to fix it.
The book also covers dealing with being interrupted by other people's requests: if you cannot do them immediately, make sure to record them or delegate to others; and make sure the requester knows what you're doing and is reassured that the request will not be forgotten. Apart from that, there is advice on how (and when) to automate tasks, how to write useful documentation so that you can delegate things instead of doing everything yourself, and even how to handle longer projects and even life goals (although without many specifics: the book is more focused on day-to-day planning).
Overall, the book offers a lot of small pieces of advice, as well as a good mindset: keep a single system of notes that you can trust instead of holding everything in memory, and make simple routines instead of wasting your attention on trying to handle everything optimally. Definitely worth a read!














